If you want to subtract two voltages, or shift a voltage while amplifying or attenuating it, the op-amp subtractor setup is ideal. An op amp and its 4 resistors allow you to subtract two voltages. This assembly makes it possible to adjust the total gain or to give a different importance to each of the two voltages (weighting coefficients that can be chosen).
Formula of the voltage in the subtractor assembly
Here is the general formula, in the general case where the 4 resistances are different.
.
Op-amp subtractor assembly: diagram and formula
The output voltage Vs depends on V2 and V1. In front of V1, there is a minus sign, which means that V1 is subtracted from V2, with coefficients linked to the values of the resistors.
The more V2 will rise, the more the output voltage Vs will rise too
The more V1 goes up, the more the output voltage Vs will go down.
Explanation of the formula of the subtractor assembly
We will explain where this foemule comes from, which may seem subtle at first.
The op amp is supposed to be ideal:
- there is no voltage between the inputs of the op amp (v + = v-).
- there is no current entering or leaving the input legs (i + = i- = 0)
In practice, this works very well with most op amps with resistances in the range of 10k to 100kOhms for frequencies below 100kHz.
To obtain the full formula of the subtracter, we are interested in only one voltage at a time, the other voltage being set to zero. Then, we add the two terms found by linearity. In electronics, this is the superposition theorem.
Subtractor assembly with zero V1
Let us study the subtractor assembly with op amp when V1 is null (connected to the mass). Zero voltage is shown schematically by a short circuit between input V1 and ground, which sets voltage V1 to zero.
.
Op amp subtractor mount with V1 connected to ground
We start by looking at part R3 and R4. R3 and R4 are nothing more than a simple voltage divider. Indeed, no current enters the op-amp by its input + (in reality, this current is negligible compared to the current which circulates in R3 and R4).
The voltage at the terminals of R4, i.e. the potential on the + input is therefore worth:
v + = V2.R4 / (R3 + R4)
Seeing the rest of the assembly, the operational amplifier is used as a non-inverting amplifier (circuit R1 and R2). The gain of the non-inverting amplifier assembly is (R1 + R2) / R1.
The output voltage Vs is therefore the result of 2 successive steps:
- attenuation by the divider R3 and R4: R4 / (R3 + R4)
- amplification by the non-inverting gain assembly: (R1 + R2) / R1
We therefore have the relation between Vs and V2:
Vs = (R4 / (R3 + R4)). ((R1 + R2) / R1) .V2
So much for the first part!
Op amp subtractor assembly with V2 connected to ground
Studying is easier. Let us suppose that V2 is null: one connects R3 to the mass. If V2 is zero, the voltage on the + input of the op amp is also zero. All the branch formed by R3 and R4 has no tension. The subtractor assembly becomes this:
.
Op amp subtractor assembly with V2 connected to ground
The voltage V1 is then amplified by a gain inverter assembly -R2 / R1 (v- = 0).
Subtractor assembly: complete formula
With the superposition theorem, the complete formula of the voltage Vs as a function of V2 and V1 is therefore worth the sum of these 2 individual results:
Vs = (R4 / (R3 + R4)). ((R1 + R2) / R1) .V2 - (R2 / R1) V1
Special cases of the op-amp subtractor assembly
If you want to do a simple voltage subtraction (difference V2 - V1), you can use common resistance values:
.
Subtractor assembly with operational amplifier
In this case, the assembly amplifies by a gain equal to R2 / R1 the difference between V2 and V1.
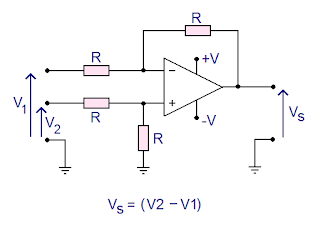
It is also possible to use only one resistance value. In this case, the output voltage Vs is equal to:
.
Subtractor op amp assembly with a single resistance value
In practice, don't forget to power the op amp! The value of R is typically between a few kOhms and a few hundred kOhms!
Applications of the op-amp subtractor assembly
Some examples of applications of the voltage subtractor:
- preamps for balanced signals (hot and cold point) such as balanced signals which pass through XLR audio cables
- voltage level offset / translation: make a voltage range compatible with an input range of a component. We can add a gain to the subtraction. For example, a sensor delivers between 6V and 8V and we want to adapt this voltage range to a range of 0V to 5V.
If you want to subtract two voltages, or shift a voltage while amplifying or attenuating it, the op-amp subtractor setup is ideal. An op amp and its 4 resistors allow you to subtract two voltages. This assembly makes it possible to adjust the total gain or to give a different importance to each of the two voltages (weighting coefficients that can be chosen).
Formula of the voltage in the subtractor assembly
Here is the general formula, in the general case where the 4 resistances are different.
.
Op-amp subtractor assembly: diagram and formula
The output voltage Vs depends on V2 and V1. In front of V1, there is a minus sign, which means that V1 is subtracted from V2, with coefficients linked to the values of the resistors.
The more V2 will rise, the more the output voltage Vs will rise too
The more V1 goes up, the more the output voltage Vs will go down.
Explanation of the formula of the subtractor assembly
We will explain where this foemule comes from, which may seem subtle at first.
The op amp is supposed to be ideal:
- there is no voltage between the inputs of the op amp (v + = v-).
- there is no current entering or leaving the input legs (i + = i- = 0)
In practice, this works very well with most op amps with resistances in the range of 10k to 100kOhms for frequencies below 100kHz.
To obtain the full formula of the subtracter, we are interested in only one voltage at a time, the other voltage being set to zero. Then, we add the two terms found by linearity. In electronics, this is the superposition theorem.
Subtractor assembly with zero V1
Let us study the subtractor assembly with op amp when V1 is null (connected to the mass). Zero voltage is shown schematically by a short circuit between input V1 and ground, which sets voltage V1 to zero.
.
Op amp subtractor mount with V1 connected to ground
We start by looking at part R3 and R4. R3 and R4 are nothing more than a simple voltage divider. Indeed, no current enters the op-amp by its input + (in reality, this current is negligible compared to the current which circulates in R3 and R4).
The voltage at the terminals of R4, i.e. the potential on the + input is therefore worth:
v + = V2.R4 / (R3 + R4)
Seeing the rest of the assembly, the operational amplifier is used as a non-inverting amplifier (circuit R1 and R2). The gain of the non-inverting amplifier assembly is (R1 + R2) / R1.
The output voltage Vs is therefore the result of 2 successive steps:
- attenuation by the divider R3 and R4: R4 / (R3 + R4)
- amplification by the non-inverting gain assembly: (R1 + R2) / R1
We therefore have the relation between Vs and V2:
Vs = (R4 / (R3 + R4)). ((R1 + R2) / R1) .V2
So much for the first part!
Op amp subtractor assembly with V2 connected to ground
Studying is easier. Let us suppose that V2 is null: one connects R3 to the mass. If V2 is zero, the voltage on the + input of the op amp is also zero. All the branch formed by R3 and R4 has no tension. The subtractor assembly becomes this:
.
Op amp subtractor assembly with V2 connected to ground
The voltage V1 is then amplified by a gain inverter assembly -R2 / R1 (v- = 0).
Subtractor assembly: complete formula
With the superposition theorem, the complete formula of the voltage Vs as a function of V2 and V1 is therefore worth the sum of these 2 individual results:
Vs = (R4 / (R3 + R4)). ((R1 + R2) / R1) .V2 - (R2 / R1) V1
Special cases of the op-amp subtractor assembly
If you want to do a simple voltage subtraction (difference V2 - V1), you can use common resistance values:
.
Subtractor assembly with operational amplifier
In this case, the assembly amplifies by a gain equal to R2 / R1 the difference between V2 and V1.
It is also possible to use only one resistance value. In this case, the output voltage Vs is equal to:
.
Subtractor op amp assembly with a single resistance value
In practice, don't forget to power the op amp! The value of R is typically between a few kOhms and a few hundred kOhms!
Applications of the op-amp subtractor assembly
Some examples of applications of the voltage subtractor:
- preamps for balanced signals (hot and cold point) such as balanced signals which pass through XLR audio cables
- voltage level offset / translation: make a voltage range compatible with an input range of a component. We can add a gain to the subtraction. For example, a sensor delivers between 6V and 8V and we want to adapt this voltage range to a range of 0V to 5V.



























No comments:
Post a Comment